Wie gross ist der Klimaeinfluss von CO2?
Von Dipl.-Ing. Peter Dietze, 2018
Offizieller (kritischer) Reviewer des IPCC-TAR, Scientific Basis, globale Strahlungs- und C-Modelle
Das Grundprinzip der Modellierung des Treibhauseffekts – sowie insbesondere der Nachweis, dass dieser so gering ist, dass keine Klimaschutzmaßnahmen erforderlich sind – ist kaum bekannt. Analysen von Beobachtungen ergeben (soweit der Einfluss von Solaraktivität und hiervon abhängiger Wolkenbedeckung berücksichtigt wird), dass eine anthropogen durch CO2 verursachte Klimakatastrophe völlig unrealistisch ist. Naheliegend ist daher die Vermutung, dass der behauptete Treibhauseffekt physikalisch vielleicht gar nicht existiert oder CO2 zumindest nur einen geringen Effekt hat.
Zur einfachen allgemeinen Erklärung (aber nicht zu Berechnungen) des Treibhauseffekts wird die Erde als eine solar beheizte, schnell rotierende sowie Wärme gut speichernde und umverteilende Schwarzkörperkugel angenommen, die somit quasi isotherm wird (die Kelvin-Temperaturen schwanken überwiegend nur im Prozentbereich). Das Problem der rotationsbedingten unbekannten und dynamischen lokalen Bodenwärmeflüsse sowie Temperaturen wird in dem Strahlungsmodell also in guter Näherung durch Mittelwertbetrachtung über die gesamte Erdoberfläche gelöst.
Da die Infrarot (IR) abstrahlende Kugeloberfläche viermal so groß ist wie der solare Einfangquerschnitt R2, wird für die Bodentemperatur nach Stefan-Boltzmann (S-B) ¼ der Solarstrahlung (Geometriefaktor 4 global anstatt 2 hemisphärisch, abzüglich 30% Albedo) genommen, was dann zu 255 K (-18 °C) führt. Und da im Mittel die Temperatur +15 Grad beträgt, folgt daraus ein „Treibhauseffekt“ von +33 Grad, der auf Gegenstrahlung von Treibhausgasen sowie Wolken zurückzuführen ist, welche ungeachtet des falsch interpretierten 2. Hauptsatzes der Thermodynamik tatsächlich gemessen wird und den solar beheizten Boden wärmer macht.
Von Interesse ist nun natürlich, um wieviel sich die Bodentemperatur erhöht, wenn sich aufgrund eines CO2-Anstiegs die IR-Absorption aus der Bodenabstrahlung und somit die Gegenstrahlung erhöht. Man kann die Stefan-Boltzmann-Formel für die thermische Abstrahlung S=σ•T4 nach der Kelvin-Temperatur T differenzieren und erhält mit dS/dT=4σ•T3 und linearisiert für kleine Änderungen der Abstrahlung (oder Einstrahlung im Gleichgewicht) können wir die Verdoppelungssensitivität wie folgt verwenden:
ΔT = AS/S/4•T
Mit S=391 W/m2 und T=288 K am Boden ergibt das +0,184 Grad pro W/m2 – und so wären wir bei einer linearen Beziehung.
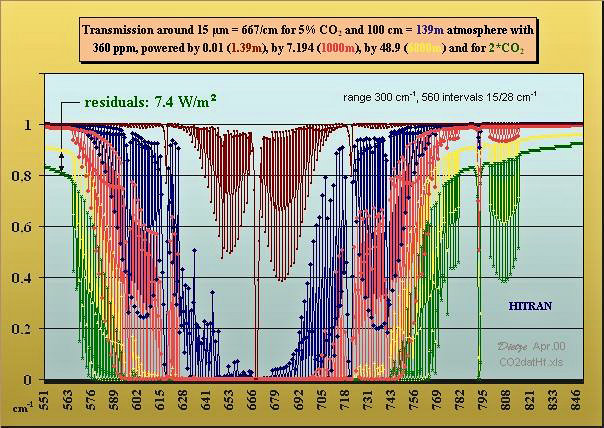
Nun benötigen wir noch den Zusammenhang mit der CO2-Konzentration. Hierzu wird der Strahlungsantrieb <1> eingeführt, der wegen der logarithmischen Abhängigkeit für jede CO2-Verdoppelung nahezu gleich groß ist und per Integration aus den Flanken der HITRAN-Spektren (Abbildung 1) bei einer globalen Bodenemission von 350 W/m2 den Wert 3,7 W/m2 ergibt. Hierbei wurde von IPCC nicht berücksichtigt, dass für die Absorption die Netto-Durchstrahlung gilt – also Bodenemission minus Gegenstrahlung (391-151=240) – weshalb der Wert um 46% zu hoch ist. Und dieser Strahlungsantrieb gilt auch nicht am Boden, sondern an TOA (top of atmosphere), und zwar ohne Wolken und Wasserdampf, was leider oft nicht beachtet wird.
Da CO2 aber unter Wolken (IR-Schwarzstrahler) weitgehend wirkungslos ist (was IPCC nicht berücksichtigt) und Wasserdampf das Spektrum überlagert – allerdings bei weitgehender Sättigung ein deutlich verringertes Feedback ergibt – und IR zwischen Boden und Atmosphäre hin- und hergestrahlt wird, wird nach einigen Korrekturen der Strahlungsantrieb am Boden 3,28 W/m2. Daraus ergibt sich „all inclusive“ eine CO2-Verdoppelungssensitivität von
ΔT = 3,28/391/4•288 = 0,6 Grad2
Wollen wir die Temperaturerhöhung (im Gleichgewicht) abhängig von einer Erhöhung der CO2-Konzentration logarithmisch berechnen (bedingt durch das Lambert-Beer’sche Gesetz, das auch in Abbildung 1 zur Anwendung kommt), so können wir die Verdoppelungssensitivität wie folgt verwenden:
ΔT = 0,6•ln(C/Co)/ln (2)
wobei C/Co das Konzentrationsverhältnis zwischen Endwert und Anfangswert ist (ist dieses 2, so ergeben sich 0,6 Grad, bei 4 werden es 1,2 Grad). Für den Anstieg von vorindustriell 280 ppm bis heute bei gut 400 ppm ergibt CO2 nur +0,31 Grad und für einen Anstieg von 400 auf 500 ppm sind es nur +0,19 Grad – das macht zusammen +0,5 Grad. 500 ppm ist die Konzentration, die wir gemäß Berechnung mit realistischen Kohlenstoffmodellen wegen einer „Halbwertszeit“ von nur knapp 40 Jahren und damit stark zunehmender Senkenflüsse höchstens noch erreichen können, wenn wir alle konventionellen fossilen Vorräte ohne Reduktion verbrennen. IPCC-Modelle nehmen – bedingt durch einen Irrtum bei der Kalibrierung gemessener Tracer-Flüsse – für die Halbwertszeit meistens einen etwa 10fach zu hohen Wert an, wodurch die Senkenflüsse viel zu gering werden und damit die zukünftigen CO2-Konzentrationen sowie Temperaturverläufe deutlich zu hoch ansteigen.
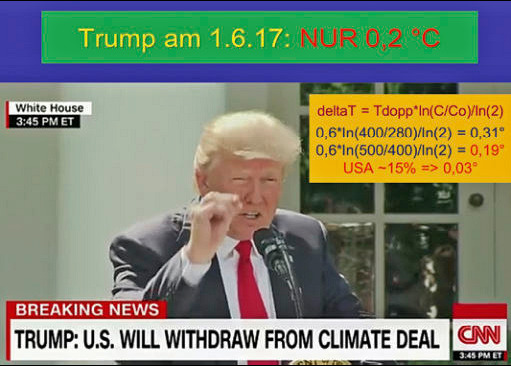
Den weiteren Temperaturanstieg von nur 0,2 °C, der bei baldiger Dekarbonisierung von 196 Ländern vermieden werden kann, hat Präsident Trump ab min 12:12 in seiner Rede am 1.6.2017 <3> als Begründung seiner wissenschaftlichen Berater für den Ausstieg aus dem Pariser Klimaabkommen 2015 genannt (Abbildung 2 mit ergänzter Berechnung nach der logarithmischen Formel). Etwa 15% der globalen Emissionen entfallen auf die USA, womit die Dekarbonisierung nur 0,03 Grad ergäbe. Für Deutschland mit etwa 2,3% wären es allenfalls 0,005 Grad – was bei Kosten von 2-3 Billionen € (!) allein für die Stromwende weder finanzierbar ist, noch mangels großer Stromspeicher technisch durchführbar erscheint, insbesondere wenn wir auch noch Elektromobilität wollen und aus der Kernenergie aussteigen.
Mit der logarithmischen Formel ergibt sich auch die Tatsache, daß das 2-Grad-Ziel einen CO2-Anstieg von 280 ppm vorindustriell auf sensationelle 2820 (!!) ppm zulässt, CO2 also nur ein Scheinproblem ist, und damit die Klimaschutz-Vereinbarungen von Paris ad absurdum geführt werden (Abbildung 3). Insbesondere gilt das auch für die zu 2 Grad ausgeführte grob falsche Berechnung eines „Restbudgets“ von etwa 700 Gt CO2 – basierend auf vermeintlich maximal 445 ppm und ca. 50% angenommenem Senkenfluß. <4> Daraus entstand irrtümlich die völlig unsinnige Forderung nach baldiger weltweiter Dekarbonisierung mit länderspezifischer Zuteilung, da dieses Restbudget – wenn wir so weitermachen wie bisher – nach etwa 19 Jahren aufgebraucht wäre. Dies wurde bereits beim G7-Gipfel 2015 auf Schloss Elmau verkündet und auch von Prof. Stocker, der IPCC-Vorsitzender werden wollte, 2016 als Grundlage für Paris in Vaduz präsentiert.
Abbildung 3 zeigt ebenfalls, dass für die in Paris 2015 eher gewünschten 1,5-Grad als Ziel (im Gleichgewicht) die maximale Konzentration 396 ppm beträgt. Offenbar war den Veranstaltern und Delegierten nicht bewusst, dass dieser Wert bereits bei der Beschlussfassung gerade überschritten war und eigentlich zu einem sofortigen Verzicht auf alle CO2-Emissionen hätte führen müssen. Dass aber nur ¼ des bisher beobachteten (transienten) Anstiegs von etwa 0,85 Grad auf CO2 zurückzuführen ist, war in Paris offenbar nicht bekannt.
Anmerkungen
<1> Der Strahlungsantrieb ist zu interpretieren als die an TOA zurückgehaltene Abstrahlung, wenn sich plötzlich die CO2-Konzentration verdoppelt – soweit noch keine Temperaturanstiege stattgefunden haben. Der Wert in W/m2 entspricht der Hälfte der zusätzlichen Absorption von 7,4 W/m2 (d.h. 3,7 W/m2 Gegenstrahlung) was sich aus HITRAN-Spektren berechnen lässt.
<2> Solch eine geringe Sensitivität ergibt sich ebenfalls bei Rechnungen mit MODTRAN. IPCC benutzt jedoch als bestguess einen irrtümlich auf Eisbohrkern-Daten (also ozeanischer Ausgasungssensitivität) basierten fünffach höheren Wert von 3 Grad, der aus einem Basiswert und extrem hohem Feedback entsteht. Man berechnet den Basiswert (stark vereinfacht, mit Hin- und Herstrahlung) aus deltaT=3,7/391/4•288/Eps, was mit Eps=240/391 am Boden 1,11 Grad ergibt (ohne Wolken, Wasserdampfüberlappung und den Feedback-Faktor 2,7).
<3> Web-Adresse: https://www.youtube.com/watch?v=djATp3AoUxI
<4> Zur Konstanthaltung bei 445 ppm wäre keine Dekarbonisierung, sondern lediglich eine Reduktion auf die angestiegenen globalen Senkenflüsse (!) von etwa 8,3 GtC/a nötig. Ähnliches gilt für die Angaben in Abbildung 2: Zur Konstanthaltung bei 400 ppm reicht eine Emissionsreduktion auf die Senkenflüsse von etwa 6,1 GtC/a. Für die USA beträgt der Anteil ca. 15%.
Literatur
Fusion, Vol. 39, 2018, Nr. 2, Seite 12 bis 14; https://www.fachinfo.eu/dietze2018.pdf
Links